Maxima has a fairly serviceable Laplace transform utility built-in. Here’s an example from the popular ordinary differential equations book by Blanchard, Devaney and Hall:

Trouble arises when we look at discontinuous forcing functions, which is especially sad because it seems to me that’s what makes it worthwhile to spend time with Laplace transforms. In particular, the inverse transform function ilt() fails on the Heaviside Function and Dirac Delta, even though the built-in laplace() treats them correctly:

So, I’ve written an alternative inverse Laplace function laplaceInv() that fixes that problem:

Here are a few differential equation solutions to show how the new function behaves:
A second-order linear equation with a constant forcing function that vanishes at


A second-order equation with two impulsive forces:

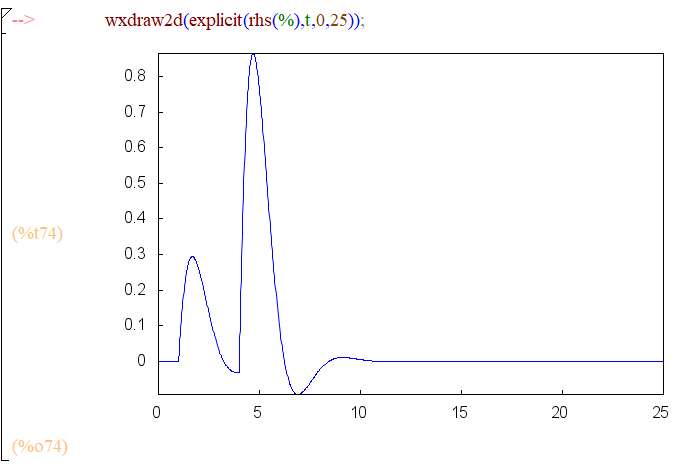
The new Laplace transform Maxima function can be downloaded here.

Thanks. I’ve had exactly the same problem when I was trying to solve few electric circuits with step input.
LikeLike
The fractional calculus, via the Laplace and Inverse Laplace Transform, is of
some value in solving differential equations and possibly circuits with non
linear components.
Might you implement this for Maxima.
LikeLike
Very useful!!
Thanks!
LikeLike
It works very well, than you so much!
LikeLike
Many thanks – this is incredibly useful to me.
LikeLike