Eulix: A Stiff ODE Solver in Maxima

Look what I found in the share/contrib directory:

There isn’t any documentation available from texinfo:

Browsing around on the web I found this documentation page.

There are also many examples given in the Eulix_*.mac files in share/contrib/Eulix . Here’s what is says at the top of Eulix.mac:

* (C) Helmut Jarausch
 *
 * @version 1.0 Date August 29th, 2017
 *
 * @author Helmut Jarausch
 *         RWTH Aachen University

 * @contents
 *  Eulix is an linearly implicit (by default) extrapolated Euler method.
 *  It uses variable step sizes, variable orders and offers dense output.
 *  Eulix can solve systems like  M y'(t)= f(t,y)  where M is a constant mass
 *  matrix. This enables the solution of differential algebraic equations (DAE)
 *  of index 1, as well.
 *
 *  I have made a simplified version of  SEULEX  published in
 *
 *  E. Hairer, G.Wanner
 *  Solving Ordinary Differential Equations II
 *  Stiff and Differential-Algebraic Problems
 *  Springer 1991

A Test Problem: The Ball of Flame

To test drive the method, I’ll retrace Cleve Moler’s steps in this excellent piece about numerical solvers for stiff equations.

We’ll consider the “ball of flame” equation of Lawrence Shampine:

\dot{y}=y^2-y^3, \;\;\;\;\;\; y(0)=\delta

on the time interval 0 \le t \le 2/\delta .

The equation is meant to be a simple model of flame propagation, but it could also describe what happens to non-stiff solvers for small values of \delta : they go down in a ball of flames!

Notice that the basic calling sequence for Eulix() is the same as for rkf45(). The first thing to observe is that when applied to the ball of flame, Eulix() uses less time and less steps than rkf45():

Plots of the solution points show that Eulix() makes this look like an easy problem, using very few points for the horizontal parts of the solution, and concentrating more points at the sharp turns:

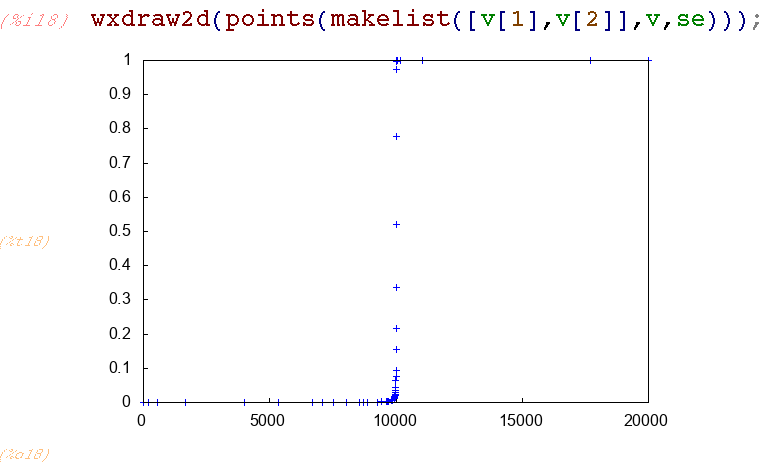
The non-stiff variable step Runge-Kutta-Fehlberg method rkf45() makes this look hard:

Zooming in shows how hard rfk45() is working on the horizontal part of the solution. It is doing its job to maintain the error within the default tolerance 1e-6, but it’s using a lot of steps and function evaluations to do that:

And one final thing to know about Eulix(): The output can appear very sparse, as we see in the region t> 10000 in the figure above. There’s an easy option to specify dense output (likely computed using splines and the existing solution points). Add the desired output interval as a fourth entry in the time specification list: [t,tstart,tfinal,output_interval]

Thank you Helmut Jarausch!

Quotes, global variables, and ODE solvers.

Computed solution: room temperature in a model of a thermostatically switched air conditioning system

Every winter term in my introductory ordinary differential equations class, I ask each of my students to choose from the scientific literature a paper that puts ODE models at the center of the work, and to reproduce the author’s results. For the past 5 years we’ve used Maxima for that purpose, and throughout the course for both symbolic and numerical tasks.

A perennial favorite is “Temperature Models for Ware Hall” by J. K. Denny and C. A. Yackel, The College Mathematics Journal, Vol. 35, No. 3 (May, 2004), pp. 162-170 http://www.jstor.org/stable/4146891 .

We have a first order ODE that combines two Newton’s law of cooling processes: the room is in thermal contact with the hot outside air at 90F and with cooled air at 60F coming from the air conditioner.

\frac{dT}{dt}=0.2(90-T)+0.2S(T)(60-T)

The idea is to model an air conditioning system that is controlled by a thermostatic switch. In the model above the switch function S(T)=1 when the cooling sytem is running, becomes zero if the system is running and the temperature reaches 67F, becomes 1 if the system is not running and the temperature reaches 73F. The behavior of the room temperature is shown in the figure at the top of this piece.

There might be another way to model this (I’d be delighted to learn what that is!) but here we treat the thermostat with a global variable that can be read and changed within a numerical solver as part of the right-hand-side function.

The question in this post is: how to implement a global flag like that in Maxima? Below are four variants involving various combinations of the Maxima quote operator. The first two give the hoped-for behavior and were used to produce the figure above. The last two don’t seem to have access to the global flag and the cooling system runs without ceasing. I include a graph of that incorrect computed solution at the bottom of this post.

The Details

  • In the first case, the switch function is included in the right-hand-side function with a single quote.
  • In the second, the switch in included with quote-quote, but the order in which the right hand side and switch is important: the switch function must be defined AFTER the right hand side function in which it is called
  • In the third, the switch in included with quote-quote, but the order from above is reversed and the global flag seems undetected.
  • In the fourth, the switch is included without quote or quote-quote and the behavior is same as quote-quote in the second and third cases.

I don’t know why each works or doesn’t! I’m hoping you do and can tell me 🙂 Thanks in advance.

/*This works as intended with single-quote on ThermSwitch
    ThermSwitch can be defined either before or after ff */
kill(all);
globalAC:1;

ThermSwitch(T):=block(
	      if T<67 then globalAC:0
	         else if T>73 then globalAC:1,
	      return(globalAC))$
		  
ff:.05*(90-T) + .2*'ThermSwitch(T)*(60-T);

s:rk(ff,T,78,[t,0,50,.1])$
wxdraw2d(points(makelist([p[1],p[2]],p,s)));
/*This works as intended with double-quote on ThermSwitch
    ThermSwitch  defined  AFTER ff */
kill(all);
globalAC:1;

ff:.05*(90-T) + .2*''ThermSwitch(T)*(60-T);

ThermSwitch(T):=block(
	      if T<67 then globalAC:0
	         else if T>73 then globalAC:1,
	      return(globalAC))$
		  
s:rk(ff,T,78,[t,0,50,.1])$
wxdraw2d(points(makelist([p[1],p[2]],p,s)));
/*This does NOT work as intended with double-quote on ThermSwitch
    ThermSwitch  defined  BEFORE ff */
kill(all);
globalAC:1;

ThermSwitch(T):=block(
	      if T<67 then globalAC:0
	         else if T>73 then globalAC:1,
	      return(globalAC))$
		  
ff:.05*(90-T) + .2*''ThermSwitch(T)*(60-T);

s:rk(ff,T,78,[t,0,50,.1])$
wxdraw2d(points(makelist([p[1],p[2]],p,s)));
/*This does NOT work as intended with unquoted ThermSwitch before ff
   it does work as intended with unquoted ThermSwitch after ff  */
kill(all);
globalAC:1;

ThermSwitch(T):=block(
	      if T<67 then globalAC:0
	         else if T>73 then globalAC:1,
	      return(globalAC))$
		  
ff:.05*(90-T) + .2*ThermSwitch(T)*(60-T);

s:rk(ff,T,78,[t,0,50,.1])$
wxdraw2d(points(makelist([p[1],p[2]],p,s)));
Incorrect Computed solution: room temperature in a model of a thermostatically switched air conditioning system — the thermostatic switch in the model isn’t functioning correctly.

Collecting all my little matlab-like Maxima widgets in one place

Since I’ve been using Maxima (circa 2016), I’ve occasionally missed some little feature from matlab and coded up a replacement for maxima, with a corresponding blog piece here at the Maximalist.

Some examples are find(), diff(), pause(), size(), cumsum(), diag(), and a few list indexing utilities. Also a help() utility that mimics matlab.

Here’s a mac file with all of those in one easy-to-load place: matlabesque.mac

Its help() entry reads like this:

matlabesque.mac contains:
 find(exp)
 ithruj(L,i,j)
 indexby(L,indexlist)
 matlab_diff(L)
 pause([options])
 cumsum(l)
 size(M)
 diag(M)
 -
 -
 for any of the above functions,
 help(function_name) returns help lines for function_name

Multiple Plots in an Animated GIF in Maxima

Here it is: Roughly the animation I wanted to create. A harmonic oscillator, with the corresponding trajectory in phase space and a bead-on-wire projection of the trajectory onto the potential energy curve.

I wanted to insert this in a powerpoint slide I would be using for an online lecture, so an animated GIF seemed like a good option. I started with an example from Dirk Mittler’s blog. (link no longer working)

What I really wanted to do was include several axes like in these examples from my earlier post at TheMaximalist, which created multiple scenes using several calls to gr2d() and then drew the scenes in a single call to draw(). The trouble I encountered was that the collection of time-synchronized multiple scenes weren’t rendered simultaneously in the animated GIF — the animation flickered back and forth between the scenes.

So I turned off the axes and made my own triplet of axes in a single scene using parametric lines and including the needed vertical offsets.

One key thing that took me a while to find: In my Windows installation (Maxima 5.44 and wxMaxima 20.06.6), no matter what I specified for a path in the file_name argument to draw(), the animated GIF file ended up getting written in C:\maxima-5.44.0

I’ve pasted the code below.

scenes: []$

for i:0 thru 61 do (
    scenes: append(scenes,
            [gr2d(proportional_axes=xy,
    noframe,
    ytics=false,xtics=false,nticks=100,
    /* oscillator 2 units below */
    color=black, 
      parametric(t,-2,t,-1.2,1.2),
    /* phase space 2 units above */
    color=black, 
      parametric(t,0,t,-1.2,1.2),
      parametric(0,t,t,-1.2,1.2),
    color=blue,
    parametric(cos(t),sin(t),t,0,2*%pi),
    /* potential */
     color=black, 
      parametric(t,2,t,-1.2,1.2),
      parametric(0,2+t,t,-.1,1),
    color=blue,
     explicit(2+x^2,x,-1.2,1.2),
    color=red,point_type=filled_circle,
        points([cos(i/10),cos(i/10),cos(i/10)],[-2,-sin(i/10),2+cos(i/10)^2]))]
        )
)$

draw(
    delay = 10,
    file_name = "oscillator_phasespace_potential",
    terminal = 'animated_gif,
    scenes
)$

C’est une pipe for Maxima

 

I really love the pipe operator $>$ introduced into R by the package magrittr.  Not least because of the reference to the piece pictured here — “The Treachery of Images” by the Belgian surrealist painter René Magritte.

I don’t know yet whether this will be a really useful Maxima feature, but it is easy enough to make a simple pipe operation using infix():

infix("%>%",1,1); 
"%>%" (a,b):=b(a);

pipe1

Notice the 2nd and 3rd arguments of infix() control the precedence of operations (the left and right hand binding powers lbp and rbp).  We want to set those values lower than lbp and rbp for multiplication * in 2*%pi  and for for addition + in 1+%i (which by default in Maxima have lbp=180 and rbp=180).  Here’s the maxima document that gives the details about operators and binding power.

To make the pipe idea slightly more powerful so as to work with functions like integrate() and diff() which require more than one argument, we could try something like this, which makes use of the matlab-like find() I wrote about recently.

infix("%>%",1,1);
"%>%" (a,b):=block([i,bb],
 if atom(b) then 
     b(a)
 else (
     i:find(b=%P),
     bb:append(firstn(b,i[1]-1),[a],rest(b,i[1])),
     apply(first(bb),rest(bb,1))
     )
);

pipe2.PNG

Note that we’ve introduced the convention that the piped expression is referred to as %P, and that we call functions using a lisp-like construction where diff(%P,x) becomes [diff,%P,x].

A MATLAB-like find() function for Maxima

In MATLAB, you can find the indices of array entries that match a user-supplied condition with the function find()

Here’s a similar function in Maxima.  This makes liberal use of the functions sublist_indices(), lambda(),  and several functions from the stringproc package: sequal(), eval_string(), and simplode().  Oh, and also the shameless hack of using ascii(32) as the space character 🙂

Here are some examples.  The code is included at the bottom.

find

find(exp):=block(
 oo:op(exp),
 if sequal(oo,"=") or sequal(oo,">") or sequal(oo,">=") or sequal(oo,"<") or sequal(oo,"<=") or sequal(oo,"#") then 
   sublist_indices(first(exp),lambda([x1],eval_string(simplode([x1,op(exp),last(exp)]))))
 else 
   if sequal(oo,"and") or sequal(oo,"or") then(
     e1:first(exp),
     e2:second(exp),
     sublist_indices(first(e1),lambda([x1],
       eval_string(simplode([x1,op(e1),last(e1),ascii(32),oo,ascii(32),x1,op(e2),last(e2)]))))
   )
)$

Two little list utilities for MATLAB-like array indexing

I grew up with MATLAB, where extracting a subset of a vector V was easy as feeding a vector of indices into a vector.  For example entries i thru j could be had with V(i:j) and an more complicated index scheme could be accomplished with a vector of indices i_index and then V(i_index).

In Maxima, first(), last(), firstn(), rest(), and most generally makelist() allows for all that and more but with a little more cumbersome calling protocols.  Here are one-liners that achieve something like the two canonical MATLAB examples above:

indexby

A maxima function to replicate MATLAB diff() and an efficiency comparison

I needed a function to compute a list containing the difference between adjacent entries in another list, as diff() does for an array in MATLAB.

I first wrote  something using makelist() and found it very slow for large lists.  I then rewrote the function using rest() and found it much faster:

differ

 

Surface Integrals, Triple Integrals, and the Divergence Theorem of Gauss in Maxima

In earlier posts, I describe the Package of Maxima functions MATH214 for use in my multivariable calculus class, with applications to Greens  Theorem and Stokes Theorem.

Here we show how the  surface integral function integrateSurf() and triple integration  function integrate3()  (together with the divergence function div() )work on a Gauss’s Theorem example:

Gauss2

We integrate the parabolic surface and the circular base surface separately, and show their sum is equal to the triple integral of the divergence.

Gauss1

The functions above are included in the MATH214 package, but I list them below as well:

integrateSurf(F,S,uu,aa,bb,vv,cc,dd):=block(
 [F2],
 F2:psubst([x=S[1],y=S[2],z=S[3]],F),
 integrate(integrate(trigsimp(F2.cross(diff(S,uu),diff(S,vv))),uu,aa,bb),vv,cc,dd));

integrate3(F,xx,aa,bb,yy,cc,dd,zz,ee,ff):=block(
 integrate(integrate(integrate(F,xx,aa,bb),yy,cc,dd),zz,ee,ff));

div(f,x,y,z):=diff(f[1],x)+diff(f[2],y)+diff(f[3],z)$

cross(_u,_v):=[_u[2]*_v[3]-_u[3]*_v[2],_u[3]*_v[1]-_u[1]*_v[3],_u[1]*_v[2]-_u[2]*_v[1]]$

 

Path Integrals in the Plane, Double Integrals, and Greens Theorem in Maxima

In an earlier post I described the Maxima package MATH214 for use in my multivariable calculus class.  I’ve posted examples with applications to Gauss’s  Theorem and Stokes Theorem.

Here we take the double integration routine integrate2() and the 2D path integral integratePathv2() for a spin with a Green’s Theorem example from Stewart’s Calculus Concepts and Contexts:

Greens2

Greens1

And of course polar coordinates are nice too:

Greens3.PNG

The two functions used above are included in the MATH214 package, but I list them below as well.

integratePathv2(H,r,t,a,b):=block(
[H2],
H2:psubst([x=r[1],y=r[2]],H),
 integrate( trigsimp(H2.diff(r,t)),t,a,b)
);

integrate2(F,xx,aa,bb,yy,cc,dd):=block(
 integrate(integrate(F,xx,aa,bb),yy,cc,dd));