Tag: surface Integral

Surface Integrals, Triple Integrals, and the Divergence Theorem of Gauss in Maxima

In earlier posts, I describe the Package of Maxima functions MATH214 for use in my multivariable calculus class, with applications to Greens  Theorem and Stokes Theorem.

Here we show how the  surface integral function integrateSurf() and triple integration  function integrate3()  (together with the divergence function div() )work on a Gauss’s Theorem example:

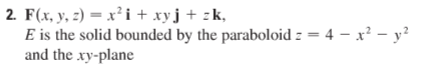
Gauss2

We integrate the parabolic surface and the circular base surface separately, and show their sum is equal to the triple integral of the divergence.

Gauss1

The functions above are included in the MATH214 package, but I list them below as well:

integrateSurf(F,S,uu,aa,bb,vv,cc,dd):=block(
 [F2],
 F2:psubst([x=S[1],y=S[2],z=S[3]],F),
 integrate(integrate(trigsimp(F2.cross(diff(S,uu),diff(S,vv))),uu,aa,bb),vv,cc,dd));

integrate3(F,xx,aa,bb,yy,cc,dd,zz,ee,ff):=block(
 integrate(integrate(integrate(F,xx,aa,bb),yy,cc,dd),zz,ee,ff));

div(f,x,y,z):=diff(f[1],x)+diff(f[2],y)+diff(f[3],z)$

cross(_u,_v):=[_u[2]*_v[3]-_u[3]*_v[2],_u[3]*_v[1]-_u[1]*_v[3],_u[1]*_v[2]-_u[2]*_v[1]]$

 

Surface Integrals and Stokes Theorem in Maxima

 

In an earlier post I detailed the Maxima functions contained  the MATH214 package for use in my multivariable calculus class.  The package at that link has now been updated with some further integration utilities:  integrate2() and integrate3() for double and triple integrals and integrateSurf() for surface integrals of vector fields in 3D.  I’ve posted examples with applications to Green’s  Theorem and Gauss’s Theorem.

Here’s a test drive of the surface integration function using a Stokes theorem example I found on the web:

Verify Stokes theorem for the surface S described by the paraboloid z=16-x^2-y^2 for z>=0

and the vector field

F =3yi+4zj-6xk

First the path integral of the vector field around the circular boundary of the surface using integratePathv3() from the MATH214 package

Stokes1

And also the surface integral using integrateSurf().  Notice that in the order of integration we specify in integrateSurf(),  (first  y then x) the surface normal vector computed with cross() in that same variable order points inward—the negative orientation.  We reverse the direction with an extra negative inside the surface integral.

Stokes2

Although they are included in the MATH214 package, here are the  functions used above:

integrateSurf(F,S,uu,aa,bb,vv,cc,dd):=block(
 [F2],
 F2:psubst([x=S[1],y=S[2],z=S[3]],F),
 integrate(integrate(trigsimp(F2.cross(diff(S,uu),diff(S,vv))),uu,aa,bb),vv,cc,dd));

cross(_u,_v):=[_u[2]*_v[3]-_u[3]*_v[2],_u[3]*_v[1]-_u[1]*_v[3],_u[1]*_v[2]-_u[2]*_v[1]]$

curl(f,x,y,z):=[ diff(f[3],y)-diff(f[2],z),curl(f,x,y,z):=[ diff(f[3],y)-diff(f[2],z),                     diff(f[1],z)-diff(f[3],x),   diff(f[2],x)-diff(f[1],y) ]$
integratePathv3(H,r,t,a,b):=block(
[H3],
H3:psubst([x=r[1],y=r[2],z=r[3]],H),
 integrate( trigsimp(H3.diff(r,t)),t,a,b)
);