In earlier posts, I describe the Package of Maxima functions MATH214 for use in my multivariable calculus class, with applications to Greens Theorem and Stokes Theorem.
Here we show how the surface integral function integrateSurf() and triple integration function integrate3() (together with the divergence function div() )work on a Gauss’s Theorem example:
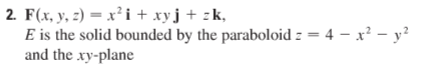
We integrate the parabolic surface and the circular base surface separately, and show their sum is equal to the triple integral of the divergence.

The functions above are included in the MATH214 package, but I list them below as well:
integrateSurf(F,S,uu,aa,bb,vv,cc,dd):=block( [F2], F2:psubst([x=S[1],y=S[2],z=S[3]],F), integrate(integrate(trigsimp(F2.cross(diff(S,uu),diff(S,vv))),uu,aa,bb),vv,cc,dd)); integrate3(F,xx,aa,bb,yy,cc,dd,zz,ee,ff):=block( integrate(integrate(integrate(F,xx,aa,bb),yy,cc,dd),zz,ee,ff)); div(f,x,y,z):=diff(f[1],x)+diff(f[2],y)+diff(f[3],z)$ cross(_u,_v):=[_u[2]*_v[3]-_u[3]*_v[2],_u[3]*_v[1]-_u[1]*_v[3],_u[1]*_v[2]-_u[2]*_v[1]]$