Category: Complex Variables

Complex roots of unity and the map() function

Here’s a little application from Complex Variables class that uses map() to repeatedly apply Maxima functions to each element in a list.

We want to find the complex 6th roots of 1 — there should be six such complex numbers z that solve the equation

  z^6=1

sixthrootseqn

Notice the solutions are returned as equations…this is sometimes really handy, but for now we want to isolate the right hand side of each equation. The command rhs(), when applied to an equation, returns just the right side. We can apply the rhs command to all the equations contained in our solution using the Maxima command map():

sixthrootsmap

Finally, with the real and imaginary parts extracted, we can plot the six roots

sixthrootsplot

 

A home-grown help utility for my Maxima functions

I have written a number of Maxima functions for my students.   I really miss the MATLAB convention by which help(functionname) prints to the console the leading comment lines in the function.  That is really easy for the developer, because the documentation lines within the function also serve as the user documentation in the console.

Maxima’s built-in documentation capabilities ?, ??, example(), demo(), and describe() are, as far as I can tell, unwieldy at best and unsuited for portable documentation to accompany user-written functions.

So, I’ve implemented my own home-grown help utility that can travel along with my *.mac files.  The scheme is:

  • Include in each *.mac file a simple help() utility that when invoked on the maxima command line as help(functionname) calls the ancillary documentation utility functionname_help() contained in the *mac file.  I’ll include this same little utility in all my *.mac files for consistency.
  • This requires that in addition to the functions themselves, the author of the functions include for each function in the *.mac file a help utility with the name convention functionname_help().
  • Upon loading of the *.mac file, I display an invitation to see the contents of the *.mac file using help(macFileName), which again requires an ancillary macFileName_help() function.  The resulting contents message also instructs in the use of the help() utility for functions.

Not as easy to implement as the MATLAB convention, but very workable from the point of view of my students as they learn to use these custom functions.

Below is an example for the ComplexVariables.mac, (which I’ll post in the next few days.)  I plan to use this as a template in all my *.mac files and I really hope the practice catches on in the Maxima community!

/*Complex Variables.mac 
Contents for use with help() */
ComplexVariables_help():=block(
printf(true,
"ComplexVariables.mac contains:
 factorC(f,z)
 partfracC(f,z)
 residueC(f,z,a)
 integratePathC(f,r,t,a,b)
 limitC(f,z,a)
 absC(exp)
 -
 -
 for any of the above functions,
 help(function_name) returns help lines for function_name"
)
);
/* The help utility */
help(_input):=block(
eval_string(sconcat(string(_input),"_help()")
)
);
/* the following is displayed upon loading */
disp("ComplexVariables.mac: help(ComplexVariables) for contents");

Visualizing Complex Functions by their images over concentric circles

A few weeks ago I posted my Maxima code for visualizing complex function by their images over a grid of line segments in the complex plane.  Here are a few images from an experiment of plotting the image of complex function over concentric circles, centered at the origin, traversed in the counterclockwise direction.  The first image below shows the identity map.  The colors are in ROYGBIV rainbow order, as noted in the legend, which gives the radius of the pre-image circles.  The second image is for the function f(z)=(z-1/2)(z-1).  Notice for the smallest radius pre-image, the image under f is largely unchanged.  As radius grows the image forms a loop then doubles on itself.  Here’s a fun insight:  that looping behavior occurs at radius .75, a circle containing a point z at which f'(z)=0.  More on this later, but its exciting to find a geometric significance of a zero of the derivative, considering how much importance such points have in real calculus.  Finally the third figure shows really interesting behavior for the function f(z)=\frac{1}{(z-1/2)(z-1)}.  Notice again the looping brought about by points at which the derivative is zero.  Notice also the change in direction of the image each time we cross over a pole—that is a root of the denominator.  The maxima code is given below.

/* wxdrawcircleC
 plot the traces of complex valued function _f
 along concentric circles |z|=r for 0<r <=1
 blue - images of _f along horizontal lines
 red - images of _f along vertical lines */
wxdrawcircleC(_f):=block(
[fx,fy,fxt,fyt,pl,j,ncirc,r,theta_shift,lm,l,dx,dy,dxy,v,nt],
ratprint:false,
fx:realpart(rectform(subst(z=x+%i*y,_f))),
fy:imagpart(rectform(subst(z=x+%i*y,_f))),
pl:[],
nt:200,
r:2,
ncirc:7,
theta_shift:%pi/20,
/* get the max modulus for computing length of arrows */
lm:0,
for n:1 thru ncirc do (
l:cons(lm,makelist(cabs(subst(z=r*n/7*exp(%i*t),_f)),t,0,2*%pi,.5)),
 lm:lmax(l)
 ),
 for j:1 thru ncirc do(
 /*first the images of the circles */
 fxt:subst([x=r*cos(t)*j/ncirc,y=r*sin(t)*j/ncirc],fx),
 fyt:subst([x=r*cos(t)*j/ncirc,y=r*sin(t)*j/ncirc],fy),
 pl:cons([parametric(fxt,fyt,t,0,2*%pi)] , pl),
 pl:cons([color=colorlist(j)],pl),
 pl:cons([key=string(r*j/ncirc)],pl),
 /* now the arrows */
 dx:subst(t=3/nt,fxt)-subst(t=0,fxt),
 dy:subst(t=3/nt,fyt)-subst(t=0,fyt),
 dxy:sqrt(dx^2+dy^2),
 v:vector([subst(t=0,fxt),subst(t=0,fyt)],[lm*dx/dxy/20,lm*dy/dxy/20]),
 pl:cons([v],pl),
 pl:cons([head_length=lm,head_angle=1],pl),
 pl:cons([color=colorlist(j)],pl),
 pl:cons([key=""],pl)
 ),
pl:cons([xlabel="",ylabel=""],pl),
pl:cons([nticks=nt],pl),
pl:cons([grid=on],pl),
apply(wxdraw2d,pl)
);

Visualizing Complex Functions with Conformal Mapping

For the thoroughly modern calculus student, an introduction to Complex Variables is all the more daunting because we don’t have the kind of geometric intuition-building machinery available to us for functions f: C \rightarrow C as we did for real-valued functions in calculus.  Not that attempts haven’t been made….  In the coming weeks, I want to work on several techniques in Maxima.  Here’s a first approach:  conformal maps.  The code drawgridC below is limited in its versatility, but couldn’t be simpler to call.  Here are some examples,

/* plot the traces of complex valued function _f
 along grid lines in the square
 -1 <= Real(z) <= 1, -1<=Ima(z)<=1
 blue - images of _f along horizontal lines
 red - images of _f along vertical lines */
drawgridC(_f):=block(
[fx,fy,fxt,fyt,pl,j,ngrid],
fx:realpart(rectform(subst(z=x+%i*y,_f))),
fy:imagpart(rectform(subst(z=x+%i*y,_f))),
pl:[],
ngrid:19,
 for j:0 thru ngrid do(
 fxt:subst([x=-1+j*2/ngrid,y=t],fx),
 fyt:subst([x=-1+j*2/ngrid,y=t],fy),
 pl:cons([parametric(fxt,fyt,t,-1,1)] , pl)
 ),
pl:cons([color=red],pl),
 for j:0 thru ngrid do(
 fxt:subst([y=-1+j*2/ngrid,x=t],fx),
 fyt:subst([y=-1+j*2/ngrid,x=t],fy),
 pl:cons([parametric(fxt,fyt,t,-1,1)] , pl)
 ),
pl:cons([color=blue],pl),
pl:cons([xlabel="",ylabel=""],pl),
pl:cons([nticks=200],pl),
apply(wxdraw2d,pl)
);

Complex Factors of Real and Complex Polynomials – part 2

Last week I posted a Maxima utility to factor polynomials using complex roots.  The idea was to use the built-in solver solve to find each root a with multiplicity m, and then construct a factor of the form (z-a)^m.  Typically, solve can fail to identify some roots that are returned by the more robust to_poly_solve.  My problem at that time was that I didn’t know how to access the multiplicities for the roots returned by to_poly_solve.

I’ve written a utility to determine multiplicities for the roots returned by to_poly_solve. With that, here’s an updated version of factorC that takes advantage of the more robust solver.

/* factor a polynomial using all its complex roots */
factorC(_f,_z):=block(
[s,n,m,fp,j],
fp:1,
ss:to_poly_solve(_f,_z),
s:create_list(args(ss)[k][1],k,1,length(ss)),
m:tpsmult1(_f,_z,ss),
/*These lines were needed before I figured out how
 how to handle multiplicities with to_poly_solve
s:solve(_f,_z),
m:multiplicities,*/
n:length(s),
for j:1 thru n do 
 if lhs(s[j])#0 
 then fp:fp*(_z-(rhs(s[j])))^m[j],
 fp:fp*divide(_f,fp)[1],
fp
);

Roots, Multiplicities, and to_poly_solve

A few days ago I posted some code to factor and perform partial fraction decomposition using all available complex roots.  The approach is to find roots a — taking note of the multiplicity m of each —  and then construct factors of the form (z-a)^m.

As I’ve noted before, the built-in command solve can fail to find solutions.  The more robust Maxima solver is to_poly_solve.    That said, after a call to to_poly_solve, I don’t know how to get my hands on the multiplicities.  So, I’ve written a little utility to compute and return a list of multiplicities for the roots returned by to_poly_solve.  Here’s an example, followed by the code.  Notice that because to_poly_solve returns solutions using the %union construction, extracting the jth root requires something like root:rhs(part(s,j,1))

tpsmult1

/* tpsmult1 assumes results of to_poly_solve applied to _f, 
 are passed in the argument s */
tpsmult1(_f,_z,s):=block(
[d,root,nroots,mult,m1],
nroots:length(s),
mult:[],
for j:1 thru nroots do (
root:rhs(part(s,j,1)),
m1:rootmult(_f,_z,root),
mult: endcons(m1,mult)
),
mult
);

/* find the multiplicity of a root _a for the polynomial _f */
rootmult(_f,_z,_a):=block(
[d,val,m,mm],
m:1,
d:divide(_f,(_z-_a)),
val:subst(_z=_a,part(d,1)),
if (val=0) then (
 mm:rootmult(part(d,1),_z,_a),
 m:m+mm
 ),
m
);

Partial Fraction Decomposition Using Complex Factors

A few days ago I wrote about my solution for factoring a polynomial into factors corresponding to complex roots,  factorC.

One of the uses for that utility is to perform a partial fractions decomposition of rational functions.  Here’s a complex partial fraction function that uses factorC and the built-in Maxima function partfrac.

partfracC

partfracC(_f,_z):=block(
[d,fd],
d:denom(_f),
fd:factorC(d,_z),
partfrac(1/fd,_z)
);

Complex Factors of Real and Complex Polynomials

I’m getting ready for my fall Complex Variables class.  I noticed that the built-in Maxima function residue doesn’t reliably do the right thing.  My goal is to make some improvements to  Maxima residue calculations in Maxima over the course of the next month.

As I started to look at some test cases, I realized I didn’t know how to factor a polynomial into complex factors.  In the simplest case:

realfactor

but I wanted to see

manual_complexfactor

Maybe someone will find this and let me know that there’s a simple way to make that happen using existing Maxima commands.  Until then, I’ve written a little utility  to identify the roots (both real and complex) of a polynomial and return a factorization.  Here’s an example, and the code.  Notice that it only works as well as the root finder solve.  I tried to upgrade to the more robust to_poly_solve,  but I don’t yet know how to handle multiplicities in that case.

factorCexample

factorC(_f,_z):=block(
[s,n,m,fp,j],
fp:1,
/* This commented code was meant to use the
more robust solver to_poly_solve, but 
I couldn't understand how to handle multiplicities
ss:args(to_poly_solve(_f,_z)),
s:create_list(ss[k][1],k,1,length(ss)),*/
s:solve(_f,_z),
m:multiplicities,
n:length(s),
for j:1 thru n do 
 if lhs(s[j])#0 
 then fp:fp*(_z-(rhs(s[j])))^m[j],
 fp:fp*divide(_f,fp)[1],
fp
);

Path Integrals

For my multivariable calculus class, I wanted an easy-to-call suite of symbolic integrators for path integrals of the form

\int_C f(x,y) dr,

\int_C {\bf F}(x,y)\cdot d{\bf r} = \int_C \langle P(x,y), Q(x,y) \rangle\cdot \langle dx, dy \rangle, or

\int_C {\bf F}(x,y,z)\cdot d{\bf r} = \int_C \langle P(x,y,z), Q(x,y,z), R(x,y,z) \rangle\cdot \langle dx, dy, dz \rangle.

My overarching design idea was that the input arguments needed to look the way they do when I teach the course:

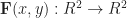  • a scalar field f(x,y):R^2 \rightarrow R or a vector field  {\bf F}(x,y): R^2 \rightarrow R^2 or {\bf F}(x,y,z): R^3 \rightarrow R^3
  • a curve C defined by a vector-valued function {\bf r}(t): R \rightarrow R^n, a\le t \le b where n=2,3 as appropriate.

It took me a while to work out how to evaluate the integrand along the path within my function.  Things that worked fine on the command line failed when embedded into a batch file to which I passed functions as arguments.  I ended up using subst, one variable at a time.  I’d like to be able to do this in a single command which can detect whether we’re in 2 or 3 dimensions so that I don’t need separate commands.

For now, here’s what I came up with along with some illustrative examples taken from Paul’s online math notes, that show how to call these new commands I, I2 and I3.

/* path integral of a scalar integrand f(x,y) on path r(t) in R^2, t from a to b */
 I(f,r,t,a,b):=block(
 [f1,f2,dr,Iout],
 f1:subst(x=r[1],f),
 f2:subst(y=r[2],f1),
 dr:sqrt(diff(r,t).diff(r,t)),
 Iout: integrate(f2*dr,t,a,b),
 Iout
 );
/* path integral of a vector integrand F(x,y) on path r(t) in R^2, t from a to b */
 I2(H,r,t,a,b):=block(
 [H1,H2,I],
 H1:subst(x=r[1],H),
 H2:subst(y=r[2],H1),
 I: integrate( H2.diff(r,t),t,a,b),
 I
 );
/* path integral of a vector integrand F(x,y,z) on path r(t) in R^3, t from a to b */
 I3(H,r,t,a,b):=block(
 [H1,H2,H3,I],
 H1:subst(x=r[1],H),
 H2:subst(y=r[2],H1),
 H3:subst(z=r[3],H2),
 I: integrate( H3.diff(r,t),t,a,b),
 I
 );

PathIntegrals

Here’s an update:  a related maxima function for evaluating a complex integral

\int_\Gamma f(z) dz

where f: C \rightarrow C and the curve \Gamma is given by r: R \rightarrow C.

/* path integral of a complex integrand f(z): C --> C, on path z(t): R --> C, t from a to b */
IC(f,r,t,a,b):=block(
[f1,dz,Iout],
f1:subst(z=r,f),
dz:diff(r,t),
Iout: integrate(f1*dz,t,a,b),
Iout
);

ComplexIntegral