Visualizing Complex Functions by their images over concentric circles

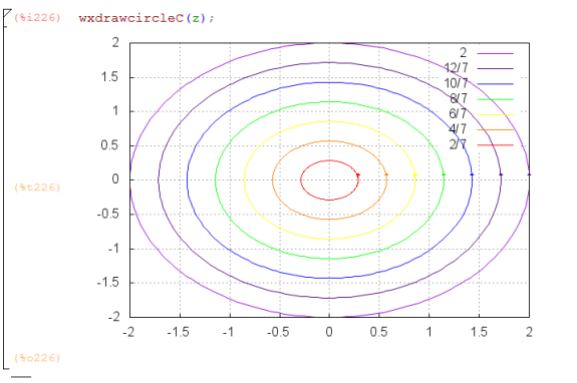
A few weeks ago I posted my Maxima code for visualizing complex function by their images over a grid of line segments in the complex plane.  Here are a few images from an experiment of plotting the image of complex function over concentric circles, centered at the origin, traversed in the counterclockwise direction.  The first image below shows the identity map.  The colors are in ROYGBIV rainbow order, as noted in the legend, which gives the radius of the pre-image circles.  The second image is for the function .  Notice for the smallest radius pre-image, the image under is largely unchanged.  As radius grows the image forms a loop then doubles on itself.  Here’s a fun insight:  that looping behavior occurs at radius .75, a circle containing a point at which .  More on this later, but its exciting to find a geometric significance of a zero of the derivative, considering how much importance such points have in real calculus.  Finally the third figure shows really interesting behavior for the function .  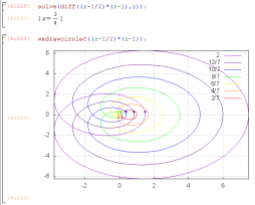Notice again the looping brought about by points at which the derivative is zero.  Notice also the change in direction of the image each time we cross over a pole—that is a root of the denominator.  The maxima code is given below.

/* wxdrawcircleC
 plot the traces of complex valued function _f
 along concentric circles |z|=r for 0<r <=1
 blue - images of _f along horizontal lines
 red - images of _f along vertical lines */
wxdrawcircleC(_f):=block(
[fx,fy,fxt,fyt,pl,j,ncirc,r,theta_shift,lm,l,dx,dy,dxy,v,nt],
ratprint:false,
fx:realpart(rectform(subst(z=x+%i*y,_f))),
fy:imagpart(rectform(subst(z=x+%i*y,_f))),
pl:[],
nt:200,
r:2,
ncirc:7,
theta_shift:%pi/20,
/* get the max modulus for computing length of arrows */
lm:0,
for n:1 thru ncirc do (
l:cons(lm,makelist(cabs(subst(z=r*n/7*exp(%i*t),_f)),t,0,2*%pi,.5)),
 lm:lmax(l)
 ),
 for j:1 thru ncirc do(
 /*first the images of the circles */
 fxt:subst([x=r*cos(t)*j/ncirc,y=r*sin(t)*j/ncirc],fx),
 fyt:subst([x=r*cos(t)*j/ncirc,y=r*sin(t)*j/ncirc],fy),
 pl:cons([parametric(fxt,fyt,t,0,2*%pi)] , pl),
 pl:cons([color=colorlist(j)],pl),
 pl:cons([key=string(r*j/ncirc)],pl),
 /* now the arrows */
 dx:subst(t=3/nt,fxt)-subst(t=0,fxt),
 dy:subst(t=3/nt,fyt)-subst(t=0,fyt),
 dxy:sqrt(dx^2+dy^2),
 v:vector([subst(t=0,fxt),subst(t=0,fyt)],[lm*dx/dxy/20,lm*dy/dxy/20]),
 pl:cons([v],pl),
 pl:cons([head_length=lm,head_angle=1],pl),
 pl:cons([color=colorlist(j)],pl),
 pl:cons([key=""],pl)
 ),
pl:cons([xlabel="",ylabel=""],pl),
pl:cons([nticks=nt],pl),
pl:cons([grid=on],pl),
apply(wxdraw2d,pl)
);